-
Mathématiques
-
Par damedubois le 17 Août 2012 à 21:10
Voici un petit jeu de familles de nombres pour rebrasser différentes représentations, inspiré d'un jeu de chez Nathan, à découper, imprimer sur du papier type bristol et à plastifier.
 Télécharger la version sans aide --> ICI
Télécharger la version sans aide --> ICI Télécharger la version avec aide (bande numérique) --> LA
Télécharger la version avec aide (bande numérique) --> LA Télécharger une version avec carte nombre (pour TataN et les autres)--> ICI
Télécharger une version avec carte nombre (pour TataN et les autres)--> ICI(images du jeu : Lakanal)
 19 commentaires
19 commentaires
-
Par damedubois le 4 Août 2012 à 14:16
 On me demande souvent ici ou ailleurs ce que j'utilise comme supports en maths. Quelle méthode, quel fichier ? En CLIS c'est assez difficile de se contenter d'une seule méthode, un mix de plusieurs approches semble plus adapté aux besoins des nos élèves. Je travaille de façon très ritualisée, vous l'aurez remarqué, mais pour que tout ça prenne du sens, situations problemes et situations complexes doivent avoir toute leur place dans l'organisation des apprentissages. Ces situations, pas besoin de les inventer, elles sont dans la plupart des ouvrages pédagogiques. Cela demande cependant du temps de repérer celles qui nous parlent, celles qui vont parler à nos élèves. Celles qui vont les aider à faire sens.Amener les élèves à construire le nombre c’est les amener à donner du sens au nombre.Connaître la suite numérique de 10 en 10 (parce que tous les jours lors du rituel on la répète avec plaisir) tout en n’étant pas capable d’isoler 5 objets d’une collection ce sont des comportements classiquement observés chez les élèves en difficultés. Tout comme savoir dire que dans 125 il y a 12 paquets des 10 sans faire le lien entre cette décomposition canonique du nombre et une situation concrète ou on demanderait combien de carnets de 10 timbres il nous faut pour en avoir 125… Avoir recours au surcomptage dès qu’une situation additive se présente ...(d’après Brissiaud c'est un marqueur de la grande difficulté et c’est un comportement classique des élèves de Segpa)…Bref, comprendre le nombre c’est à la fois savoir à quoi il sert et comment il fonctionne. L’un va difficilement sans l’autre et quand c’est le cas, les compétences observées ne sont pas transférables.J'avais tenté un petit blabla théorique sur l’évaluation en maths LA. Je vais essayer de lister ici quelques situations qu'on pourrait qualifier "de référence" dans l'apprentissage du nombre au cycle 2 ainsi que les ouvrages pédagogiques dans lesquels on peut les trouver plus détaillées. Ce terme de situation de référence, je pense qu'il ne faut pas l'entendre comme situation incontournable, obligatoire (ce qui serait bien culpabilisant si on ne les mettait pas en place dans nos classes)… mais plutot comme une situation que l’on peut proposer et à laquelle on pourra "faire référence" par la suite pour aider les élèves à faire du lien entre les activités : "Rappelle toi, cette soustraction c’est comme quand on fait le jeu du greli-grelo… "Le nombre est un outil pour résoudre des problèmes...vous trouverez cette définition du nombre dans de multiples ouvrages. D’où l’idée de donner des problemes à résoudre à nos élèves ;) et d'organiser les progression pour les aider à passer d'une résolution non numérique à une résolution mettant forcement en œuvre le nombre (Je me rappelle qu'à l'IUFM je me demandais bien comment ils allaient l'avoir cette révélation. En observant nos zozos, on me rend bien compte que ce n'est absolument pas miraculeux et que sans y mettre des mots, de l'explicite, on ne fixe rien, et que malheureusement c'est souvent cette phase de mise en mot, d'"institutionnalisation" qui pêche dans nos séances).Si on se base sur ce schéma récapitulant les 3 fonctions du nombre, on peut détailler pour chacune d'elle quelques situations intéressantes.Le but du jeu au cycle 2 serait de passer de situations pouvant être résolues sans faire appel au nombre à des situations ou il va devenir nécessaire de mettre en œuvre autre chose que du terme à terme, de l'appariement de collections. On organise les progressions pour aider les élèves à passer d'une résolution non numérique à une résolution mettant forcement en œuvre le nombre. Cela passe par une augmentation des quantités, une mise a distance des collections à comparer, un délai dans le temps qui incitera à utiliser le nombre en tant que symbole. (Je me rappelle qu'à l'IUFM je me demandais bien comment ils allaient l'avoir cette révélation. En observant nos zozos, on me rend bien compte que ce n'est absolument pas miraculeux et que sans y mettre des mots, de l'explicite, on ne fixe rien, et que malheureusement c'est souvent cette phase de mise en mot, d'"institutionnalisation" qui pêche dans nos séances...).
On me demande souvent ici ou ailleurs ce que j'utilise comme supports en maths. Quelle méthode, quel fichier ? En CLIS c'est assez difficile de se contenter d'une seule méthode, un mix de plusieurs approches semble plus adapté aux besoins des nos élèves. Je travaille de façon très ritualisée, vous l'aurez remarqué, mais pour que tout ça prenne du sens, situations problemes et situations complexes doivent avoir toute leur place dans l'organisation des apprentissages. Ces situations, pas besoin de les inventer, elles sont dans la plupart des ouvrages pédagogiques. Cela demande cependant du temps de repérer celles qui nous parlent, celles qui vont parler à nos élèves. Celles qui vont les aider à faire sens.Amener les élèves à construire le nombre c’est les amener à donner du sens au nombre.Connaître la suite numérique de 10 en 10 (parce que tous les jours lors du rituel on la répète avec plaisir) tout en n’étant pas capable d’isoler 5 objets d’une collection ce sont des comportements classiquement observés chez les élèves en difficultés. Tout comme savoir dire que dans 125 il y a 12 paquets des 10 sans faire le lien entre cette décomposition canonique du nombre et une situation concrète ou on demanderait combien de carnets de 10 timbres il nous faut pour en avoir 125… Avoir recours au surcomptage dès qu’une situation additive se présente ...(d’après Brissiaud c'est un marqueur de la grande difficulté et c’est un comportement classique des élèves de Segpa)…Bref, comprendre le nombre c’est à la fois savoir à quoi il sert et comment il fonctionne. L’un va difficilement sans l’autre et quand c’est le cas, les compétences observées ne sont pas transférables.J'avais tenté un petit blabla théorique sur l’évaluation en maths LA. Je vais essayer de lister ici quelques situations qu'on pourrait qualifier "de référence" dans l'apprentissage du nombre au cycle 2 ainsi que les ouvrages pédagogiques dans lesquels on peut les trouver plus détaillées. Ce terme de situation de référence, je pense qu'il ne faut pas l'entendre comme situation incontournable, obligatoire (ce qui serait bien culpabilisant si on ne les mettait pas en place dans nos classes)… mais plutot comme une situation que l’on peut proposer et à laquelle on pourra "faire référence" par la suite pour aider les élèves à faire du lien entre les activités : "Rappelle toi, cette soustraction c’est comme quand on fait le jeu du greli-grelo… "Le nombre est un outil pour résoudre des problèmes...vous trouverez cette définition du nombre dans de multiples ouvrages. D’où l’idée de donner des problemes à résoudre à nos élèves ;) et d'organiser les progression pour les aider à passer d'une résolution non numérique à une résolution mettant forcement en œuvre le nombre (Je me rappelle qu'à l'IUFM je me demandais bien comment ils allaient l'avoir cette révélation. En observant nos zozos, on me rend bien compte que ce n'est absolument pas miraculeux et que sans y mettre des mots, de l'explicite, on ne fixe rien, et que malheureusement c'est souvent cette phase de mise en mot, d'"institutionnalisation" qui pêche dans nos séances).Si on se base sur ce schéma récapitulant les 3 fonctions du nombre, on peut détailler pour chacune d'elle quelques situations intéressantes.Le but du jeu au cycle 2 serait de passer de situations pouvant être résolues sans faire appel au nombre à des situations ou il va devenir nécessaire de mettre en œuvre autre chose que du terme à terme, de l'appariement de collections. On organise les progressions pour aider les élèves à passer d'une résolution non numérique à une résolution mettant forcement en œuvre le nombre. Cela passe par une augmentation des quantités, une mise a distance des collections à comparer, un délai dans le temps qui incitera à utiliser le nombre en tant que symbole. (Je me rappelle qu'à l'IUFM je me demandais bien comment ils allaient l'avoir cette révélation. En observant nos zozos, on me rend bien compte que ce n'est absolument pas miraculeux et que sans y mettre des mots, de l'explicite, on ne fixe rien, et que malheureusement c'est souvent cette phase de mise en mot, d'"institutionnalisation" qui pêche dans nos séances...).1-Le nombre "mémoire de la quantité "
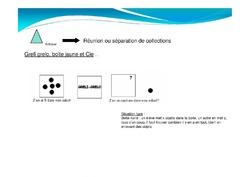
--> Réaliser une collection qui a autant d’éléments qu’une collection de référence --> Compléter une collection pour qu’elle ait autant d’éléments qu’une collection de référence
--> Compléter une collection pour qu’elle ait autant d’éléments qu’une collection de référence --> Réaliser une collection qui doit être le double, le triple…d’une collection de référence
--> Réaliser une collection qui doit être le double, le triple…d’une collection de référence --> Comparer des collections
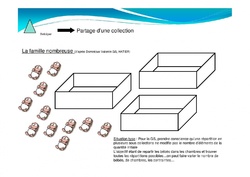
--> Comparer des collections 2-Le nombre "mémoire du rang "
2-Le nombre "mémoire du rang "--> Mémoriser la place d’une objet dans une série
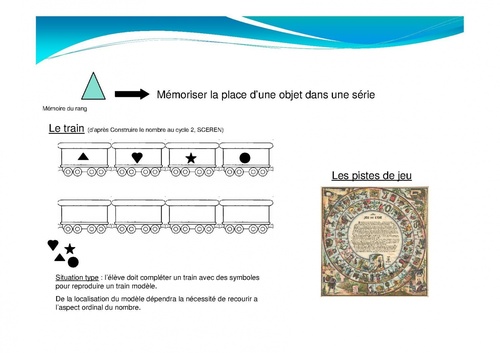
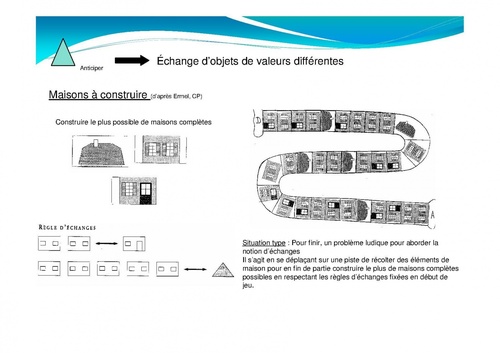
3-Le nombre "pour anticiper"
Cette liste n'est bien sure pas exhaustive. Elle s'appuie sur le découpage proposé dans les ERMEL et reprend ce que j'ai aimé mettre en place dans ma classe. Vous connaissez et utilisez surement d'autres activités, dont l'habillage est différent mais qui font travailler les mêmes compétences.Cette dernière situation est une bonne transition pour passer à une 2eme aspect du nombre, le nombre en tant qu'objet de savoir...A venir d'autres exemples pour travailler cet aspect avec vos élèves.Les images de cet article peuvent être retrouvées sur le site de ma circonscription : ICI. 11 commentaires
11 commentaires
-
Par damedubois le 4 Août 2012 à 11:00
Un petit up pour ce rituel ;) (article originalement publié en octobre 2011)
Voici un petit rituel que mes élèves adorent : il leur permet de parler d’eux-mêmes sans que cela vire au quoi de neuf interminable tout en faisant des maths sans s’en rendre compte. C’est un des rituels que je mettais en place dans ma classe en Louisiane, où au delà de l’aspect mathématiques de la chose, il permettait de faire beaucoup parler les élèves en français !
Deux fois par semaine, je griffonne un petit dessin au tableau pour symboliser le thème du jour. Rien que ça mes zozos adorent : ils essayent de deviner quelle va être la question à partir des symboles qu’ils reconnaissent…
Je commence en général par répondre moi-même à la question, puis chacun leur tour les élèves prennent la parole. Je garde une trace des réponses selon un code qui varie selon le type de question et selon mon objectif du moment.
Par exemple :
Pour analyser ce tableau, on compte combien d’élèves en tout ont un ordinateur, combien d’élèves n’en ont pas… En faisant la somme de ces deux nombres on vérifie que l’on obtient bien le nombre de personnes présentes en classe ce jour là.
Pour certaines questions, on peut garder une trace sous forme de diagramme de Venn.
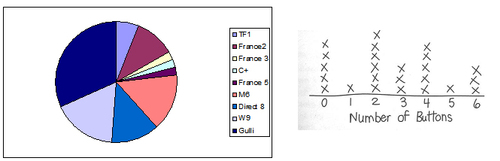
Pour d’autres, un diagramme en bâton sera plus intéressant.
Sur cet exemple, on peut faire remarquer aux élèves quel est le mois o ù il y a le plus d’anniversaire, celui o ù il y en a le moins…Toujours en vérifiant bien que le total des cases grisées correspond au nombre de personnes participant au jeu.
Pourquoi ne pas élargir le « pannel » et poser des questions aux autres classes… Avec une question apparemment sans intérêt, comme « combien y a-t-il de boutons sur ta tenue aujourd’hui ? » ou d’autres plus « concrètes » comme « quelle chaîne de télévision as-tu regardé hier » on peut obtenir divers types de graphique et faire des statistiques sans en avoir l’air …
Nous construisons petit à petit, à une échelle tout modeste, diverses façons d’organiser des données et de les analyser. Pour les aider à prendre conscience que cela peut les aider à résoudre des problèmes de la vie courante, j'utilise parfois ce rituel pour régler des questions concernant la vie de classe comme "entre ces trois albums, lequel voulez-vous que je lise demain ?" ou "quelle recette de gâteau préférez-vous réaliser ce mois-ci ?".
 Si vous lisez l'anglais voici un petit lien rigolo -- > ICI
Si vous lisez l'anglais voici un petit lien rigolo -- > ICI A venir un autre petit jeu pour faire des probabilités l'air de rien
A venir un autre petit jeu pour faire des probabilités l'air de rien  -- > Coming soon.
-- > Coming soon. Enfin, si vous tentez dans votre classe, laissez-moi en commentaires les questions qui ont le mieux fonctionné pour vos élèves ! Merci d'avance!
Enfin, si vous tentez dans votre classe, laissez-moi en commentaires les questions qui ont le mieux fonctionné pour vos élèves ! Merci d'avance! Un lien vers les idees de DixMois -- > ICI
Un lien vers les idees de DixMois -- > ICI 4 commentaires
4 commentaires
-
Par damedubois le 4 Décembre 2011 à 14:19
Voici une petite vidéo dénichée par mon CPC-ASH, qui résume en quelques mots et en images les théories de Brissiaud sur la conceptualisation des nombres.
 2 commentaires
2 commentaires
-
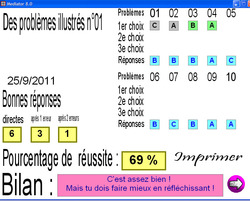
Par damedubois le 25 Septembre 2011 à 15:38
Je vous renvoie aujourd'hui au superbe travail de mon cher collègue de CM1. Il s'agit d'une banque d'exercices très bien conçue pour travailler la résolution de problèmes. Réalisés avec Mediator, leur utilisation ne demande aucun logiciel specifique, il suffit de lancer les exercices sur votre ordinateur pour pouvoir les tester ou de les installer pour les proposer à vos élèves.
Un des grands avantages de ces petits programmes, c'est la fiche de résultats qui permet de laisser les élèves en autonomie tout en conservant une trace de leurs réussites et difficultés afin d'y revenir par la suite si nécessaire.
 Voici le lien --> 18 programmes pour le raisonnement
Voici le lien --> 18 programmes pour le raisonnement 3 commentaires
3 commentaires
-
Par damedubois le 24 Septembre 2011 à 17:10
Voici une petite compilation de jeux à partir du "château" des nombres. Ce sont des activités que nous faisons régulièrement à l'oral en grand groupe dès que le tableau de "chaque jour compte" commence à se remplir. Elles permettent aux élèves de comprendre et d'utiliser (en particulier pour calculer mentalement) l’algorithme de la suite numérique ecrite.
A télécharger ICI (en version Show) et LA en version modifiable (PowerPoint). N’hésitez pas à me signaler les bugs si vous en trouvez !
 13 commentaires
13 commentaires
-
Par damedubois le 22 Septembre 2011 à 21:44
Je propose régulièrement à mes élèves de jouer en autonomie sur les ordinateurs de la classe. J'ai pour cela à disposition de nombreux diaporamas PowerPoint (lisibles sous OpenOffice), que ma cop's Marie m'avait transmis il y a 3 ans. J'ai commencé cet été à les refaire à ma sauce. Voici celui de "la maison du dix".
 Télécharger le diaporama --> LA
Télécharger le diaporama --> LAPour obtenir une version modifiable,
laissez moi un p'tit mot, c'est maintenant disponible ICI. 10 commentaires
10 commentaires
-
Par damedubois le 19 Août 2011 à 14:35


Qu’est ce qu’un nombre, comment l’enfant construit ce concept et comment nos évaluations peuvent-elles prendre en compte les différentes données théoriques ? J’ai tenté de résumer les réponses à ces questions lors de la rédaction de mon mémoire CAFIPEMF. A priori je n'ai pas raconté trop de bêtises
 alors je me permets de mettre en ligne ces quelques réflexions, si ça vous aide faites-le moi savoir!
alors je me permets de mettre en ligne ces quelques réflexions, si ça vous aide faites-le moi savoir! Le nombre est un outil qui a trois fonctions principales : Les fonctions premières du nombre sont de mémoriser la quantité et le rang. Il permet aussi d’anticiper le résultat d’une action sans avoir à la réaliser.
Le nombre est un outil qui a trois fonctions principales : Les fonctions premières du nombre sont de mémoriser la quantité et le rang. Il permet aussi d’anticiper le résultat d’une action sans avoir à la réaliser. Le nombre est un langage avec ses signes et ses règles : Au cours de l’histoire, l’humanité a inventé divers systèmes pour écrire le nombre. La numération de position en base 10 (ou décimale) est un de ces systèmes.
Le nombre est un langage avec ses signes et ses règles : Au cours de l’histoire, l’humanité a inventé divers systèmes pour écrire le nombre. La numération de position en base 10 (ou décimale) est un de ces systèmes. Le nombre est un objet sur lequel on peut opérer : De par les relations qui existent entre eux, les nombres permettent la comparaison, le partage et le calcul.
Le nombre est un objet sur lequel on peut opérer : De par les relations qui existent entre eux, les nombres permettent la comparaison, le partage et le calcul. Pourquoi trouve-t'on souvent dans les évaluations des exercices de logique ?
Pourquoi trouve-t'on souvent dans les évaluations des exercices de logique ?On se place dans une optique piagetienne. Jusqu’aux années 1980, ce sont les théories de Piaget, qui dominent pour expliquer comment les enfants construisent le nombre. Le concept de nombre n’est élaboré qu’autour de 7 ans, quand l’enfant est capable de concevoir une totalité comme une composition de parties. Pour cela trois structures logiques sont nécessaires :
 Pourquoi évalue-t'on classiquement les capacités de nos élèves à reconnaître « spontanément » des constellations, des configurations de doigts.
Pourquoi évalue-t'on classiquement les capacités de nos élèves à reconnaître « spontanément » des constellations, des configurations de doigts. Des expérimentations ont montré l’existence de capacités « numériques » chez de très jeunes enfants, comme par exemple la discrimination entre deux petites quantités, ou la capacité d’énumérer automatiquement des petites quantités : le subitizing. Attention : dès que l’on dépasse 3 ou 4, ce n’est apparement plus vraiment de la reconnaissance globale qui se met en œuvre, mais une décomposition/recomposition du nombre très rapide.
 D’où viennent les questionnaires et les pistes pour observer les élèves en train de dénombrer des collections ?
D’où viennent les questionnaires et les pistes pour observer les élèves en train de dénombrer des collections ?Une des compétences essentielle est la maîtrise de l’énumération, on observe pour cela la coordination œil / doigt / chaîne numérique orale. D’autres exercices sont basés sur les recherches de Gelman qui attribue au comptage un rôle prépondérant dans la construction du nombre. Elle avance en 1983 l'idée que l'enfant naît avec une connaissance implicite des « principes du comptage ».
Les principes du comptage d’après Gelman : comptage d’une collection d’objets
1) principe d’ordre stable : les mots nombres sont engendrés dans le même ordre à chaque comptage
2) principe de correspondance terme à terme : chaque élément est désigné par un mot nombre et un seul
3) principe cardinal : le dernier mot nombre prononcé représente la quantité à dénombrer
4) principe d’abstraction : faire abstraction de la nature des objets de la collection à dénombrer
5) principe de non-pertinence de l’ordre : l’ordre de comptage n’affecte pas le résultat
 Quelles références derrière les exercices pour évaluer les représentations du nombre ?
Quelles références derrière les exercices pour évaluer les représentations du nombre ?Le travail de
Fuson est parfois utilisé (quand on demande de compter a rebours, ou entre deux bornes…): pour lui, c'est dans la variété des contextes de comptage avec l’adulte et en quatre étapes successives que l’enfant va s’approprier la chaîne numérique.Les cinq niveaux de l’apprentissage de la chaine verbale d’après Fuson
1) le chapelet : les mots nombres n’ont pas d’individualité (12345)
2) la chaîne insécable: impossibilité de compter à partir d’un autre nombre que 1
3) la chaîne sécable : possibilité de compter d’un nombre à un autre
4) la chaîne dénombrable et unitaire : comptage à rebours, annonce du nombre précédent
5) la chaîne terminale : nombres traités comme des éléments distincts
Le lien entre représentation écrites et orales est un incontournable des évaluations. On peut s’appuyer sur les travaux de S.Baruk, qui a écrit sur le rôle des mots dans la construction du nombre. Les travaux de Brissiaud donnent des pistes pour évaluer la compréhension de la valeur des chiffres selon leur position, des notions de groupements et d’échanges.
 Pourquoi s'interroger sur les relations entre les nombres, pourquoi du calcul dans une évaluation de numération ?
Pourquoi s'interroger sur les relations entre les nombres, pourquoi du calcul dans une évaluation de numération ?Avec par exemple des exercices d’ajout ou de retrait d’éléments d’une collection, la connaissance du répertoire additif, des exercices de comparaisons ou des problèmes numériques, on peut se référer a Brissiaud, pour qui c’est par la maîtrise de ces relations qu’une conceptualisation du nombre est possible.
 Quel est l'intérêt de s’interroger sur le sens que les élèves donnent au nombre?
Quel est l'intérêt de s’interroger sur le sens que les élèves donnent au nombre?Par l’intermédiaire de questionnaires, en observant dans quelles situations l’élève utilise le nombre plutôt que l’appariement terme à terme on fait du lien avec les travaux de l’équipe d’ERMEL. Ils indiquent que l’enfant conceptualise le nombre en l’utilisant d’abord comme un outil pour résoudre des problèmes puis comme un objet de connaissance, pouvant être étudié pour lui-même.
 Sur le site « IdéesASH » vous trouverez des évaluations très bien conçues, qui s’articulent explicitement avec les données théoriques sur la construction du nombre (merci Fanny46 pour le lien!) : ICI
Sur le site « IdéesASH » vous trouverez des évaluations très bien conçues, qui s’articulent explicitement avec les données théoriques sur la construction du nombre (merci Fanny46 pour le lien!) : ICI Quelques références bibliographiques : BARUK Stella. 1997. Comptes pour petits et grands. MAGNARD
BERDONNEAU Catherine, 2006. Aider les élèves en difficultés en mathématiques. HACHETTE
BRISSIAUD Remi, 2003. Comment les enfants apprennent à calculer. RETZ
BRISSIAUD Remi, 2007. Premiers pas vers les maths. RETZ
SCEREN, 2009. Le nombre au cycle 2. Ressources pour faire la classe
Sur le web : ICI
CHAROTTE Fabienne, EMPIRIN Fabien et RAJAN Claude, 2001. Nombres et calcul. BORDAS
ERMEL, 2005. Apprentissages numériques et résolution de problèmes. CE1. HATIER
ERMEL, 1990. Apprentissages numériques et résolution de problèmes. GS. HATIER
FAYOL Michel 1990. L’enfant et le nombre : du comptage à la résolution de problèmes. DELACHAUX et NIESTLE
 5 commentaires
5 commentaires Suivre le flux RSS des articles de cette rubrique
Suivre le flux RSS des articles de cette rubrique Suivre le flux RSS des commentaires de cette rubrique
Suivre le flux RSS des commentaires de cette rubrique