Situations problèmes de référence pour construire le nombre au cycle 2

04.08.2012

On me demande souvent ici ou ailleurs ce que j'utilise comme supports en maths. Quelle méthode, quel fichier ? En CLIS c'est assez difficile de se contenter d'une seule méthode, un mix de plusieurs approches semble plus adapté aux besoins des nos élèves. Je travaille de façon très ritualisée, vous l'aurez remarqué, mais pour que tout ça prenne du sens, situations problemes et situations complexes doivent avoir toute leur place dans l'organisation des apprentissages. Ces situations, pas besoin de les inventer, elles sont dans la plupart des ouvrages pédagogiques. Cela demande cependant du temps de repérer celles qui nous parlent, celles qui vont parler à nos élèves. Celles qui vont les aider à faire sens.

Amener les élèves à construire le nombre c’est les amener à donner du sens au nombre.

Connaître la suite numérique de 10 en 10 (parce que tous les jours lors du rituel on la répète avec plaisir) tout en n’étant pas capable d’isoler 5 objets d’une collection ce sont des comportements classiquement observés chez les élèves en difficultés. Tout comme savoir dire que dans 125 il y a 12 paquets des 10 sans faire le lien entre cette décomposition canonique du nombre et une situation concrète ou on demanderait combien de carnets de 10 timbres il nous faut pour en avoir 125… Avoir recours au surcomptage dès qu’une situation additive se présente ...(d’après Brissiaud c'est un marqueur de la grande difficulté et c’est un comportement classique des élèves de Segpa)…

Bref, comprendre le nombre c’est à la fois savoir à quoi il sert et comment il fonctionne. L’un va difficilement sans l’autre et quand c’est le cas, les compétences observées ne sont pas transférables.

J'avais tenté un petit blabla théorique sur l’évaluation en maths LA. Je vais essayer de lister ici quelques situations qu'on pourrait qualifier "de référence" dans l'apprentissage du nombre au cycle 2 ainsi que les ouvrages pédagogiques dans lesquels on peut les trouver plus détaillées. Ce terme de situation de référence, je pense qu'il ne faut pas l'entendre comme situation incontournable, obligatoire (ce qui serait bien culpabilisant si on ne les mettait pas en place dans nos classes)… mais plutot comme une situation que l’on peut proposer et à laquelle on pourra "faire référence" par la suite pour aider les élèves à faire du lien entre les activités : "Rappelle toi, cette soustraction c’est comme quand on fait le jeu du greli-grelo… "

Le nombre est un outil pour résoudre des problèmes...vous trouverez cette définition du nombre dans de multiples ouvrages. D’où l’idée de donner des problemes à résoudre à nos élèves ;) et d'organiser les progression pour les aider à passer d'une résolution non numérique à une résolution mettant forcement en œuvre le nombre (Je me rappelle qu'à l'IUFM je me demandais bien comment ils allaient l'avoir cette révélation. En observant nos zozos, on me rend bien compte que ce n'est absolument pas miraculeux et que sans y mettre des mots, de l'explicite, on ne fixe rien, et que malheureusement c'est souvent cette phase de mise en mot, d'"institutionnalisation" qui pêche dans nos séances).

Si on se base sur ce schéma récapitulant les 3 fonctions du nombre, on peut détailler pour chacune d'elle quelques situations intéressantes.

Le but du jeu au cycle 2 serait de passer de situations pouvant être résolues sans faire appel au nombre à des situations ou il va devenir nécessaire de mettre en œuvre autre chose que du terme à terme, de l'appariement de collections. On organise les progressions pour aider les élèves à passer d'une résolution non numérique à une résolution mettant forcement en œuvre le nombre. Cela passe par une augmentation des quantités, une mise a distance des collections à comparer, un délai dans le temps qui incitera à utiliser le nombre en tant que symbole. (Je me rappelle qu'à l'IUFM je me demandais bien comment ils allaient l'avoir cette révélation. En observant nos zozos, on me rend bien compte que ce n'est absolument pas miraculeux et que sans y mettre des mots, de l'explicite, on ne fixe rien, et que malheureusement c'est souvent cette phase de mise en mot, d'"institutionnalisation" qui pêche dans nos séances...).

1-Le nombre "mémoire de la quantité "

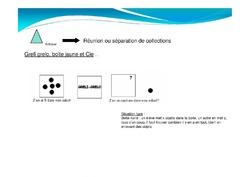
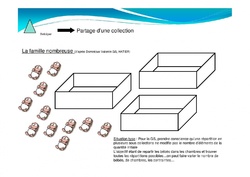
--> Réaliser une collection qui a autant d’éléments qu’une collection de référence Situations problèmes de référence pour construire le nombre au cycle 2

Situations problèmes de référence pour construire le nombre au cycle 2

--> Compléter une collection pour qu’elle ait autant d’éléments qu’une collection de référence

--> Réaliser une collection qui doit être le double, le triple…d’une collection de référence

--> Comparer des collections

2-Le nombre "mémoire du rang "

--> Mémoriser la place d’une objet dans une série

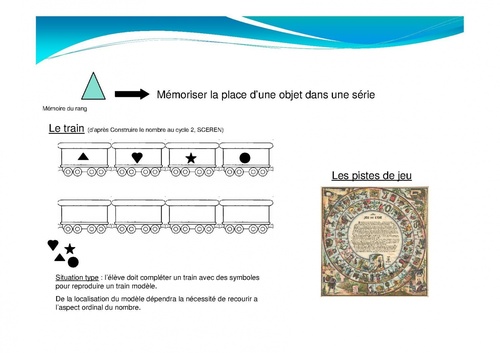
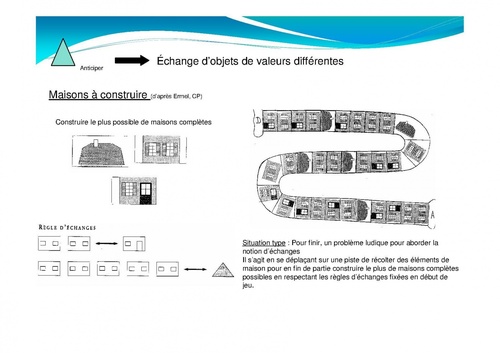
3-Le nombre "pour anticiper"

--> Le résultat de la réunion ou de la séparation de collections

--> Le résultat du partage d'une collection

--> Le résultat d’échanges d'objets de valeurs différentes

Cette liste n'est bien sure pas exhaustive. Elle s'appuie sur le découpage proposé dans les ERMEL et reprend ce que j'ai aimé mettre en place dans ma classe. Vous connaissez et utilisez surement d'autres activités, dont l'habillage est différent mais qui font travailler les mêmes compétences.

Cette dernière situation est une bonne transition pour passer à une 2eme aspect du nombre, le nombre en tant qu'objet de savoir...A venir d'autres exemples pour travailler cet aspect avec vos élèves.

Les images de cet article peuvent être retrouvées sur le site de ma circonscription : ICI.